Forum adverts like this one are shown to any user who is not logged in. Join us by filling out a tiny 3 field form and you will get your own, free, dakka user account which gives a good range of benefits to you: No adverts like this in the forums anymore. Times and dates in your local timezone. Full tracking of what you have read so you can skip to your first unread post, easily see what has changed since you last logged in, and easily see what is new at a glance. Email notifications for threads you want to watch closely. Being a part of the oldest wargaming community on the net. If you are already a member then feel free to login now.

So the Hyper-Progenitive special rule allows a Tervigon to reroll 1's when spawning Gaunts. I was thinking about this and how it affects total number of gaunts spawned.

Tervigon rules are:
1. spawn 3D6 gaunts
2. any doubles = no more spawns

for 3 dice there are 216 combinations ( 6 combinations on each dice = 6x6x6)
Doubles wise there are:
6 combinations where all 3 dice match
30 combinations where dice 1 and dice 2 match (but dice 3 doesn't) - 6 combinations that match * 5 combinations of the other dice
30 combinations where dice 2 and dice 3 match (but dice 1 doesn't)
30 combinations where dice 1 and dice 3 match (but dice 2 doesn't)
= 96/216
= 44.44% chance that you cannot spawn any more gaunts
(edit: previously had wrong denominator in this calculation)

But if you reroll 1s then it feels like you are more likely to get duplicates. Lets test the theory with heads/tails where you reroll tails
So there are 9 possible combinations:
Heads + Heads = 0.5 * 0.5 = 0.25 (DOUBLE)
Heads + Tails->Heads = 0.5 * 0.25 = 0.125 (DOUBLE)
Heads + Tails->Tails = 0.5 * 0.25 = 0.125
= 0.5

Tails->Heads + Heads = 0.25 * 0.5 = 0.125 (DOUBLE)
Tails->Heads + Tails->Heads= 0.25 * 0.25 = 0.0625 (DOUBLE)
Tails->Heads + Tails->Tails = 0.25 * 0.25 = 0.0625
=0.25

Tails->Tails + Heads = 0.25 * 0.5 = 0.125
Tails->Tails + Tails->Heads = 0.25 * 0.25 = 0.0625
Tails->Tails + Tails->Tails = 0.25 * 0.25 = 0.0625 (DOUBLE)
=0.25

= 0.625 = 62.5% chance of double

So if you re-roll one result there is less variation in the numbers that come up so there is a higher chance of duplication? For coin flipping the chance of double goes from 50% to 62% (if my maths is correct!)

Now the question for Tervigons (and I think this is beyond my maths) is 'do you get more gaunts on average when rerolling 1's or does the higher chance of getting doubles cancel it out?'

Just realized this is going to get worse if it's 'may reroll 1s'... and you decide to only reroll if you have a double 1 (and obviously only re-roll of those dice).

I would say the only use of that is on the occasion your doubles are ones. Any other situation it sounds like a bad idea.

I feel like your math might be a little off, because listing them as dice one 2 and 3 puts them in an order and uses permutations, but order isnt important so we should be using combinations. So we would want to use statements like "An outcome where 2 or more dice match has 36 possible outcomes." This already includes triples in 6 of those 36. If 2 dice have 6 outcomes where there are doubles, (1,1) (2,2) (3,3) (4,4) (5,5) & (6,6), then we just scale that up once dice and multiply it by 6,

Meaning 36/216 is the probability of rolling doubles. Thats 16.67% .

6 of those outcomes involve double ones, so 30/216 --> 13.89% of doubles with no reroll. Right?

Couple of things. First if I remember correctly, you don't have the option to not reroll 1s. You must reroll them. This will increase your chances of tapping out... the real advantage here is not being required to take the mass blob of gaunts to take the tervigon out of hq slots. You still have to take 30 gaunts, but they are broken up and so can be more useful for holding objectives, and you re still left with 2 hq slots open for better options. In my opinion its worth the extra chance to tap out.

Axxion51 wrote:
I feel like your math might be a little off, because listing them as dice one 2 and 3 puts them in an order and uses permutations, but order isnt important so we should be using combinations. So we would want to use statements like "An outcome where 2 or more dice match has 36 possible outcomes." This already includes triples in 6 of those 36. If 2 dice have 6 outcomes where there are doubles, (1,1) (2,2) (3,3) (4,4) (5,5) & (6,6), then we just scale that up once dice and multiply it by 6,

Meaning 36/216 is the probability of rolling doubles. Thats 16.67% .

6 of those outcomes involve double ones, so 30/216 --> 13.89% of doubles with no reroll. Right?

The OP is fine with his math. If you have a hard time with that, imagine he's rolling 3 dice of different colors and you're rolling 3 dice that are all of the same color. The OP is working out the possible combinations of how the different colored dice could come up, but the probability of him rolling doubles is the same as of you rolling doubles.

You're correct in that there is an issue of permutation vs. combination here, but the OP dealt with it properly.

</mathteacher>

I've only done a quick 'back of a cigarette packet' calculation, and may have missed something, but I reckon the chance is not much different - up to 45.92%

An easy way to confirm the probability of doubles is to calculate the probability to get no doubles.

With 1d6 we got 6/6 = 100% chance for no doubles (quiet simple)

If we ve got 2d6 we can throw a single die to get our first number. The second die have a 5/6 chance to differ from the first number, so we ve got a 5/6 chance for no doubles.

If we ve got 3d6 the first two dice got our 5/6 probability to show a different number. So there are only 4 numbers left for the third die to differ from the other ones.

So its 5/6 *4/6 = 20/36 to get no doubles. Therefore we ve got a 16/36 =44,4% chance of rolling a double... easy, isnt it?

Wow thanks for the schooling! That seems way more likely than I assumed it would be to roll doubles on 3 dice.

Here are some fancy tables, figures and numbers. I ran this just after it first came out:


I wanted to see what this does to the number. My first thought is that you are going to be spawning more on the first turn, but you'll get an increased likelihood of failing to spawn again. After running the numbers...



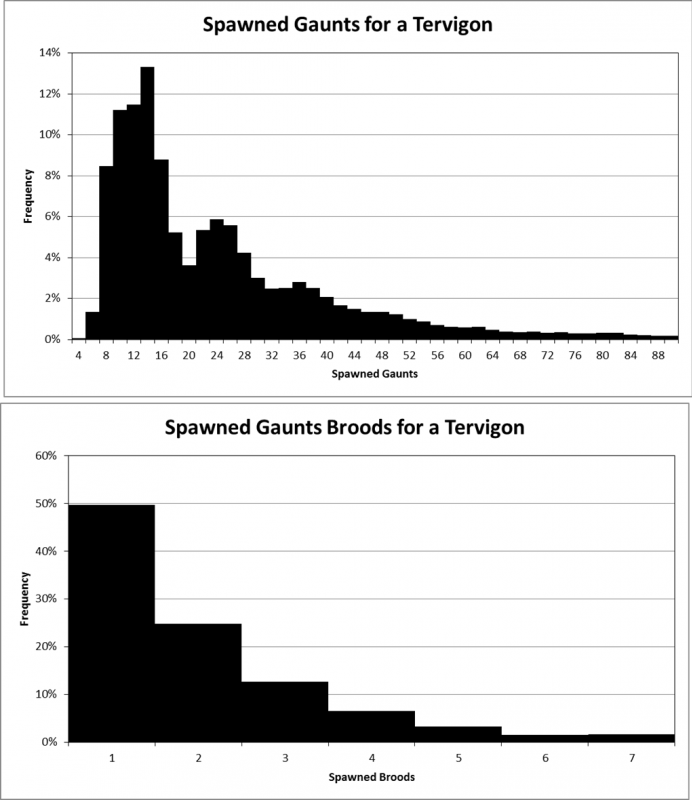
One thing you can see here is that the number of 1 brood spawned went up by 6%, so that confirmed one of my theories.



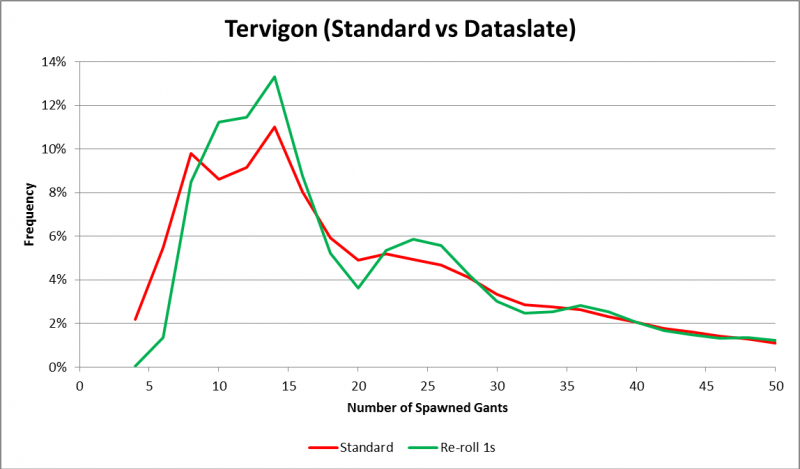
Comparing this to the last one, we see a strange dip at around 19 gants. This is because 18 being the maximum amount that can be spawned in one turn happens more often since you're re-roll 1s.

Finally:



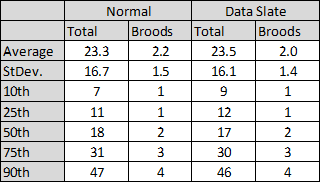
As expected. You will spawn very slightly less broods and gants.

There is one benefit this brings. It will lower the number very small gant squads. That right there may make the change worth it. You're still going to have to take some more troops (2 warrior broods maybe).